中心趋势的描述性统计测量

Key words: Descriptive Statistic, measure of central tendency ,statistic, parameter, mean(μ) ,median, mode

• 统计量：它是根据样本数据计算的描述性度量。一般的流程是构建统计量去估计总体的参数！

• 参数： 它是根据总体数据计算的描述性度量。

• n ：代表样本的数量。

• N：代表总体的数量。

• 描述中心趋势的统计量有：平均数、中位数、众数、偏度（skewness）

• 平均数(mean): 数据的平均值。

  • $$\bar{x} = \sum_{i=1}^n \frac{x_i} {n}$$

  • 特点：

    1. 唯一性
    2. 简单性 3. 易受极端值的影响

• 中位数(median): 唯一性，简单性，不易受极端值的影响

• 众数(mode): 有时它并不是唯一的，它可用于描述定性数据。

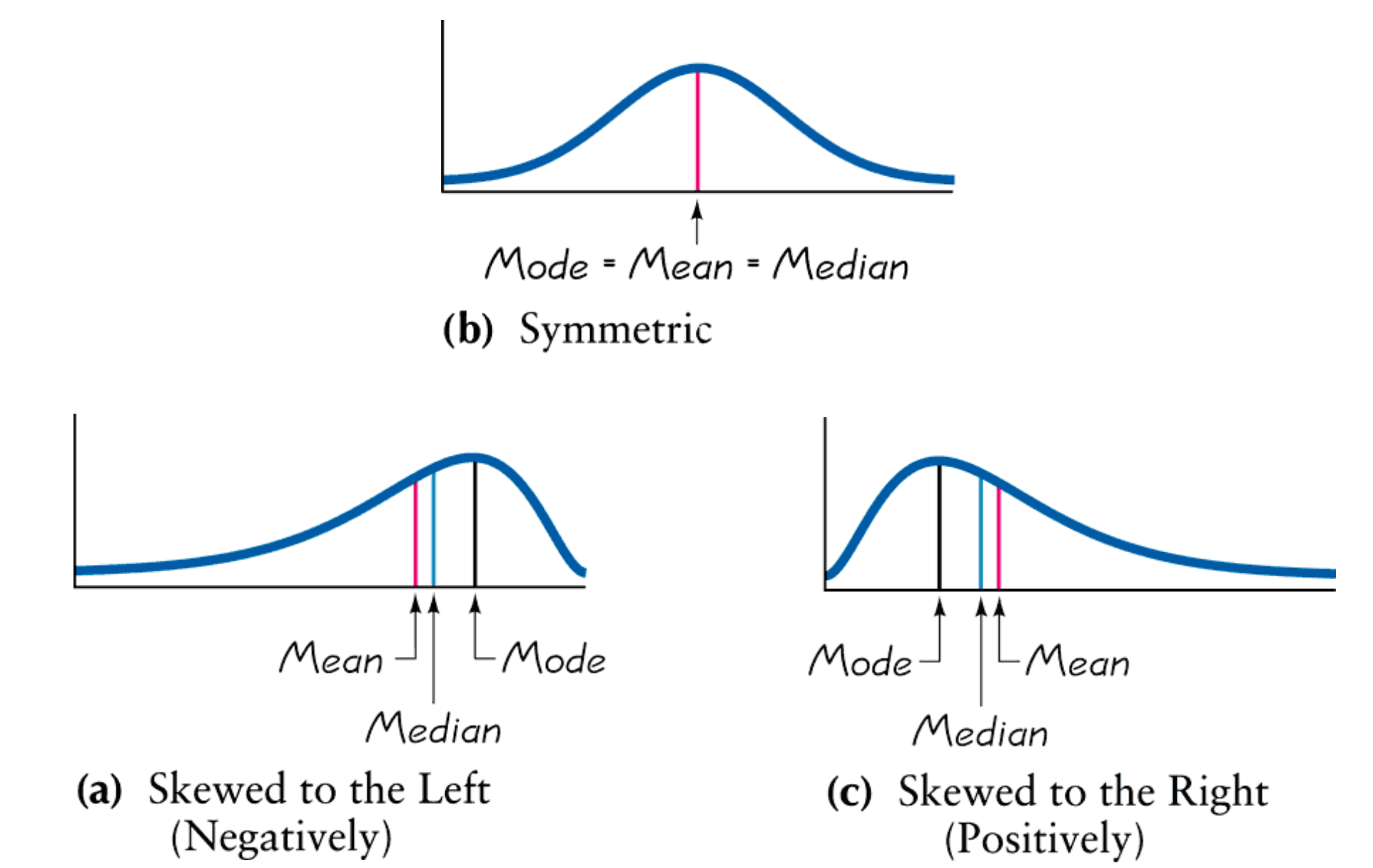
• 对称性(Symmetric): 如果数据的直方图的左半部分大致是其右半部分的镜像，则数据是对称的。

• 偏移(Skewed): 如果数据不对称，并且数据延伸到一侧的程度大于另一侧，则数据会发生偏斜。

  

分散度的描述性统计量

Key wordsDescriptive Statistic, measure of dispersion , range ,variance, coefficient of variation.

• 分散度(dispersion)：分散度量传达关于一组数据中存在的可变性的信息。

  1. If all the values are the same → There is no dispersion .

  2. If all the values are different → There is a dispersion:
  3. If the values close to each other →The amount of Dispersion small.
  4. If the values are widely scattered → The Dispersion is greater.

• 分散度的描述：

  1. Range (R).

  2. Variance.
  3. Standard deviation.
  4. Coefficient of variation (C.V).

• 范围(range): Range = Largest value- Smallest value $X_L-X_S$

• 方差(variance):

  • 总体方差： $σ^2 = \sum_{i=1}^N \frac{(x_i-μ)^2}{N}$

  • 样本方差： $S^2 = \sum_{i=1}^n \frac{(x_i-\bar{x})^2}{n-1}$

• 变异系数/The Coefficient of Variation (C.V) :它是用于比较两组数据中的分散度，其与 测量单位无关。

  ​ $C.V=\frac{S}{\bar{x}}$

概率论—统计推断的基础

Key words: Probability, Objective Probability,Subjective Probability, Equally likely,Mutually exclusive, Multiplicative rule,Conditional Probability, Marginal probability, Independent events, Bayes theorem .

• 等价(Equally likely outcomes): 事件有着相同的发生概率。
• 互斥事件(Mutually exclusive): 两个事件不可能同时发生。
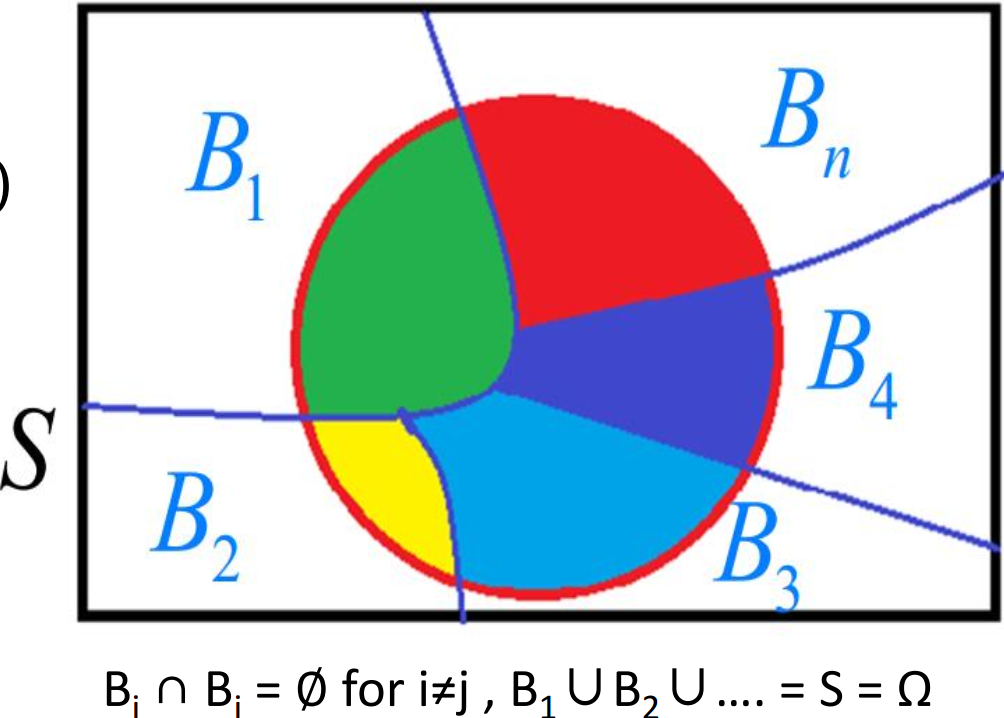
• 全集(The universal Set (S)): 所有能够发生事件的集合。
• 空集(empty set) :Φ。

• 古典概型(Classical Probability): 古典概型也叫传统概率、其定义是由法国数学家拉普拉斯 (Laplace ) 提出的。 如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型。 在这个模型下，随机实验所有可能的结果是有限的，并且每个基本结果发生的概率是相同的。

• 相对频率(Relative Frequency Probability: ) 另一种经典的概率方法是相对频率，即单个事件的发生与结果总数的比率。 这是一种在收集数据后经常使用的工具。 您可以将数据的单个部分与收集的数据总量进行比较。
• 主观概率(Subjective Probability)主观概率是一种概率，来源于个人对特定结果是否可能发生的个人判断。 它不包含正式的计算，只反映了主题的观点和过去的经验。

概率的基本属性

1. $$P(E_i) >= 0, i= 1,2,3,……n$$
2. $$P(E_1) + P(E_2) +……+P(E_n )=1$$
3. $$P(E_i +E_j )= P(E_i)+ P(E_j), where E_i ,E_j \ are\ mutually\ exclusive$$

概率的计算规则

1. 加法规则 $P(A \cup B)= P(A) + P(B) – P (A \cap B )$

2. 如果事件A和B互斥，那么加法法则简化成： $P(A \cup B)= P(A) + P(B)$

3. 互补规则： $P(\bar{A})= 1- P(A)$

概率期望

期望是线性的。

1. 离散随机变量的期望：

$$E[x]=\sum_{i=1}^\infty x_ip_i$$

1. 连续随机变量的期望： $E[x]=\begin{matrix} \int_{-\infty}^{\infty} xf(x)\, dx\end{matrix}$

$$E[X+C]=E[X]$$ $$E[X+Y]=E[X]+E[Y]$$ $$E[aX]=a×E[X]$$

1. 方差(二阶矩 second moments)的计算： $Var[x]=E[X^2]-(E[X])^2$

2. n 阶矩： $E(X^n )= \sum X_i^np_i$

3. n阶中心矩： $E((X-μ)^n )= \sum (X_i-μ)^np_i$

4. 累积矩(Cumulant )： $\frac{E((X-μ)^n )}{\sigma^n}$

条件概率

$$P(A|B)=\frac{P(A \cap B)}{P(B)} \ ,P(B)\not=0$$

乘法公式 Multiplicative Rule

$$P(AB) = P(B)·P(A|B) = P(A)·P(B|A)$$ $$P(A_1A_2…A_{n-1}A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)…P(A_n|A_1A_2…A_{n-1})$$

P(A),P(B):边际概率(marginal probability )

全概率 formula of total probability

$$P(A)=\sum_{k=1}^n P(AB_k)=\sum_{k=1}^n P(A|B_k)P(B_k)$$

全概率: 由所有已知(n个)原因B推断结果A 。

独立事件

事件A对事件B的发生没有影响。

1. $$P(A\cap B)= P(B)P(A)$$
2. $$P(A|B)=P(A)$$
3. $$P(B|A)=P(B)$$

边际概率

$$P(A_i)=\sum_{j=1}^n P(A_iB_j)$$

贝叶斯公式

全概率公式“由原因推结果”； 而贝叶斯公式“由结果推原因” $P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^n P(B_j)P(A|B_j)}$

---

• Previous
  细胞周期
• Next
  seq2seq

---